Types of Controller | I, D, PD, P, PI, PID Control

Introduction

A controller is like the boss of a control system. It’s responsible for keeping everything running smoothly. Think of driving a car and wanting to stay at a certain speed. The controller is like your foot on the gas pedal, making sure you stay at that speed.

If the car’s speed isn’t right, the controller steps in to fix it. It checks the difference between the speed you want and the actual speed (called the error signal) and adjusts the gas pedal to get you back on track.

Basically, the controller makes sure things work the way you want by making small tweaks as needed. It’s like having someone always watching and fixing things to keep everything going smoothly.

Read Also

Controller | Types of Controller, Applications, and Primary Terminologies

Controllers are like the brains of systems, ensuring they work smoothly. There are different types:

1. On/Off: Simple, like a light switch.
2. Proportional (P): Adjusts based on current need.
3. Integral (I): Corrects past mistakes.
4. Derivative (D): Predicts future needs.
5. Proportional-Integral (PI): Balances quick response and accuracy.
6. Proportional-Derivative (PD): Focuses on stability and anticipation.
7. Proportional-Integral-Derivative (PID): Combines all for precise, efficient control. These controllers are used in various industries to keep processes running smoothly.

Types of Controller

Process controls are tools used to manage things like temperature, level, and pressure. PID controllers are a type of controller that keeps adjusting the output to match what’s needed. For example, in a temperature controller for a tank, a sensor measures the temperature, compares it to the desired temperature, and adjusts a heating coil to get it right. This kind of control, where adjustments are based on the difference between what’s happening and what’s wanted, is called error-based control. PID controllers are a common type of error-based control. Before getting into how PID controllers work, it’s important to understand the concepts of feed-forward and feedback control.

P, I, D, PI, PD, PID Control

Controllers come in different types, like proportional, integral, and derivative (PID) controllers. They all work by connecting the difference between what’s happening and what’s wanted (the error) to what needs to be done (the actuating signal). PID controllers can use one or a combination of these methods to get the job done.

1. Proportional (P) Control

Proportional control is a basic method of feedback control. It works by adjusting the system based on how far off it is from the desired point. While it can respond quickly, it doesn’t always get the system exactly where it needs to be, leaving a small difference called an offset. This offset can be reduced but not eliminated by combining proportional control with other methods.

c(t) = K_ce(t) + b

where,

• c(t) = controller output
• Kc = controller gain
• e(t) = error
• b = bias

In this equation, the bias and controller gain are numbers that define how a controller behaves. The bias is what the controller output is when there’s no error. The controller gain shows how much the output changes for a given change in the input. For PID controllers, which often deal with electronic signals, the gain relates to how much the output voltage changes compared to the input voltage. This voltage change affects properties like temperature or pressure.

If the output changes more than the input, the gain is more than 1; if the input changes more, the gain is less than 1. Ideally, with a super high gain, we could reduce the error to zero, but that can make the system unstable. So, there’s a limit to how high the gain can be.

In P-only control, the controller output changes in a straight line with the error. It helps the system settle down without any extra bouncing around, getting it back to a stable state. The controller looks at the difference between the desired and actual values, calculates the error, and then figures out what to do based on that and the bias. The graph of a P-controller’s output looks just like a step input graph, showing how the system responds to a sudden change in input.

Let’s imagine a tank where a P-only controller is used to control the level of a fluid. At first, the amount of fluid coming into the tank is the same as the amount leaving it. But if the outflow decreases, more fluid enters than leaves, causing the level to rise. The P-controller adjusts the outflow until it matches the inflow, bringing the level back to normal. However, it doesn’t return to the exact initial level—it stabilizes at a new level. This difference between the initial level and the new one is called the P-control offset.

2. Integral (I) Control

Integral control, another type of feedback control, is used to eliminate deviations in the system, returning it to its original setting and steady state. It responds to accumulated past errors, adjusting the system based on the total error over time. It’s slower than proportional control but helps maintain precise control within a narrow range. However, it can destabilize the controller and cause integrator windup, delaying changes.

c(t) = 1T_i ∫ e(t)dt + c(t₀)

where,

• c(t) = is the controller output
• Ti = is the integral time
• e(t) = is the error
• c(t0) = is the controller output before integration

The above equation describes how integral control works. It’s about the time it takes for the controller to adjust its output based on the error. The controller’s output before integration is either the initial output or the output just before the measurement.

In integral control, the rate of change in the controller’s output depends on a few factors, including the error (e) and the integral time (Ti). Unlike proportional control, where the output changes linearly with the error, integral control uses an integral to calculate the response. This means it takes longer for the controller to figure out the right adjustment.

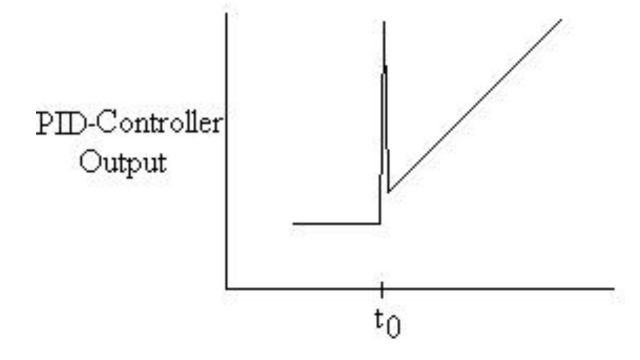
Just like with proportional control, integral control looks at the set point, the actual signal, and the bias. It calculates the error and sends it to the algorithm. But instead of a linear relationship, it uses an integral to decide the response. This process takes longer because it considers the error over time. The graph of an I-controller’s output for a step increase in input looks like the area under the step input graph.

3. Derivative (D) Control

Derivative control, another type in PID controllers, is a form of feed-forward control. It predicts system changes by analyzing how quickly the error is changing. Its main job is to dampen sudden changes and oscillations, helping to keep the system stable. The control output is based on the rate of change of the error over time.

Unlike proportional and integral control, derivative control doesn’t bring the system to a steady state on its own. It’s usually used alongside proportional, integral, or both to effectively manage the system.

In derivative control, the controller output is related to how fast the error is changing. It looks at how the error changes over time. This process is shown in Equation.

c(t) = T_d . de / dt

where,

• c(t) = is the controller output
• Td = is the derivative time constant
• de = is the differential change in error
• dt = is the differential change in time

Graphical representations of how these variables affect the system are shown in PID Tuning via Classical Methods.

Derivative control is the opposite of integral control. While there are I-only controls, there are no D-only controls. Derivative control focuses solely on how the error is changing over time. It doesn’t know where the setpoint is, so it’s often used along with proportional or a combination of proportional and integral control.

Derivative control is best for systems where the process outputs change rapidly. However, it’s more complex mathematically than proportional control. Since calculating derivatives takes longer than simply relating input and output variables, using derivative control can slow down the controller’s response time.

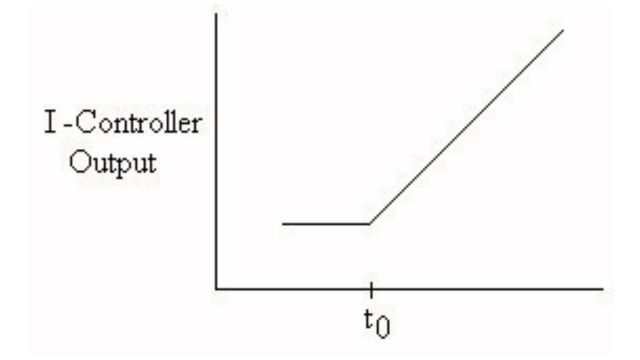
A graph of a D-controller’s output for a step increase in input shows the derivative of the step input graph. This means it shows how fast the input is changing over time.

4. Proportional-Integral (PI) Control

PI control, a combination in PID systems, doesn’t include derivative control. It’s a type of feedback control that combines proportional and integral actions. PI control responds faster than integral-only control because it includes proportional action. It helps stabilize the system and brings it back to the set point. However, it’s slower than proportional-only control, about 50% slower. To speed up response time, PI control is often paired with derivative-only control.

In PI control, the controller output depends on both the error and the integral of the error. This combination is shown in Equation.

c(t) = K_c (e(t) + 1Ti ∫e(t)dt) + C

where

• c(t) = is the controller output,
• Kc = is the controller gain,
• Ti = is the integral time,
• e(t) = is the error, and
• C = is the initial value of the controller

In this equation, the integral time represents how long it takes for the integral part of the controller to catch up with the control provided by the proportional part.

Essentially, the PI controller is like a simplified version of a PID controller without the derivative term. It’s a blend of proportional and integral control. In this setup, the bias term in proportional control is equivalent to the integral action in integral control. Proportional control kicks in when the system isn’t at the set point, while integral control takes over when the system reaches the set point. If the system deviates from the set point again, proportional control comes back into play.

A graph of a PI controller’s output for a step increase in input looks like a combination of the graphs for proportional and integral control.

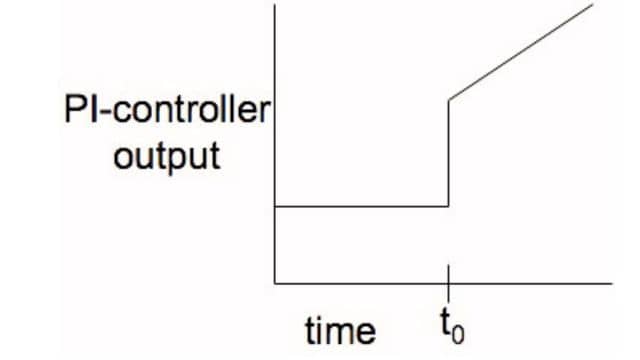
5. Proportional-derivative (PD) Control

PD control, another combination in PID systems, doesn’t include integral control. It’s a mix of feedforward and feedback control, taking into account current and predicted process conditions. In PD control, the controller output is a combination of the error signal and its derivative. This means it considers both how much the error is right now and how fast it’s changing.

In simple terms, PD control combines the damping effect of proportional control, which reduces fluctuations, with the predictive ability of derivative control, which anticipates process errors. This combination helps stabilize the system and improve its response.

The mathematical equation for PD control shows how the controller output is determined based on the error and its derivative.

c(t) = K_c (e(t) + Td . de / dt) + C

where,

• c(t) = controller output
• Kc = proportional gain
• e = error
• C = initial value of the controller

The equation shows that PD control works like a simplified version of PID control without the integral term. Alternatively, it can be seen as a blend of proportional and derivative control. In PD control, the derivative part predicts errors to enhance system stability. However, PD control isn’t commonly used because it lacks the integral term, which minimizes error in a steady state. It’s mainly used in batch pH control loops, where steady-state error isn’t a big concern. In these setups, the error is related to the controller output through both proportional and derivative terms.

Graphically, the output of a PD controller for a step increase in input looks like a mix of proportional and derivative control graphs.

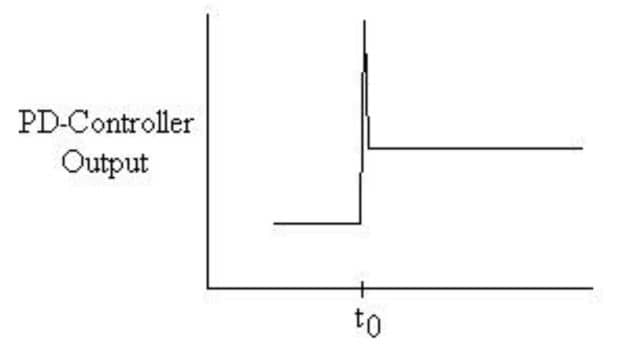
6. Proportional-Integral-Derivative (PID) Control

PID control combines proportional, integral, and derivative control methods. It’s the most common because it offers the benefits of all three.

Proportional control provides a quick response, while integral control eliminates or reduces steady-state error. Derivative control predicts disturbances, improving stability.

The PID controller’s output is determined by considering the error, the integral of the error, and the derivative of the error. This mathematical relationship is shown in Equation.

c(t) = K_c (e(t) + 1 / Ti ∫e(t)dt + Td . de / dt) + C

where,

• c(t) = controller output
• Kc = controller gain
• e(t) = error
• Ti = integral time
• Td = derivative time constant
• C = initial value of the controller

The equation demonstrates that PID control combines proportional, integral, and derivative actions. In this equation, the gain affects all three actions. However, PID control isn’t suitable for processes with a lot of noise, as it relies on predictive aspects that can be affected by noise. It’s used when the process needs fast response time and no offset.

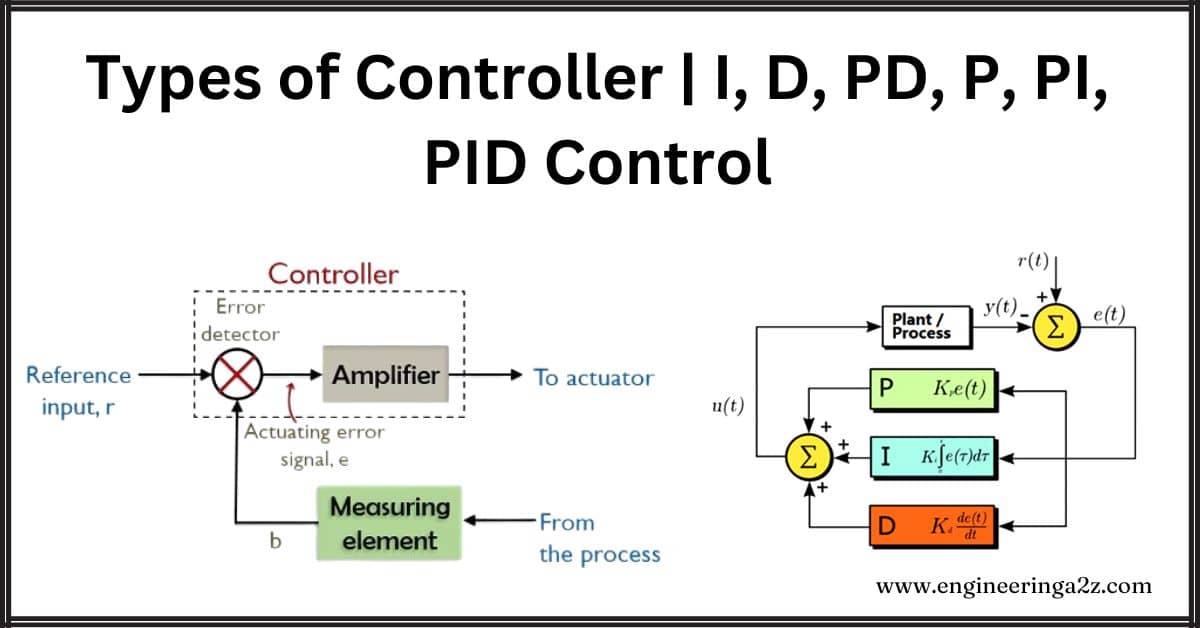
Graphically, the output of a PID controller for a step increase in input looks like a blend of proportional, integral, and derivative control graphs.

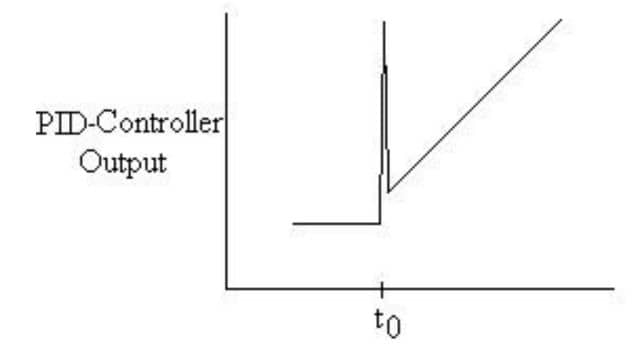
In addition to control, the P-, I-, and D- controls can be combined in other ways. These alternative combinations are simplifications of the PID control.

Frequently Asked Questions (FAQs)

Read Also:

• Diode | Construction, Working, Types, and Application
• Linear Applications of Op-Amp
• Feedback Amplifier | Types, Properties, and Topologies
• DIAC | Construction | Working and V-I Characteristics
• TRIAC | Construction, Working And V-I Characteristics

Read More>>>>